Chapter 3 The Cox Regression Model

library(survival)
library(tidyverse)
library(flexsurv)
library(rms)
library(skimr)

3.1 Inngangur

Þessi kafli fjallar um Cox líkanið sem er aðhvarfsgreiningarlíkan. Við viljum færa okkur yfir í afhvarfsgreiningu til að meta áhrifsstærðir og til að geta leiðrétt fyrir skýribreytum (explanatory variables). Aðhvarfsgreining hefur þá möguleika umfram einföld próf til að bera saman hópa.

Log-rank prófið segir okkur bara að munur sé á lifun milli hópa en ekki hve mikill hann er. Hægt er að leiðrétta með því að gera stratified próf. En ekki hægt að leiðrétta fyrir samfelldum breytum.

3.2 Modeling the hazard function

Markmiðið er að búa til líkan fyrir hættuföllin þ.e. hazard föllin og lýsa hvernig bakgrunnsreytur hafa áhrif á þau. Tökum dæmi úr sýnidæmi 1.3 sem fjallar um lifun sjúklinga með multiple myeloma

Survival_of_multiple_myeloma_patients <- read.table("Data/Survival of multiple myeloma patients.dat",
                                                    header=T)
d_1_3 <- Survival_of_multiple_myeloma_patients

Skýribreyturnar þar eru:

names(d_1_3)[-c(1:3)]

## [1] "age"     "sex"     "bun"     "ca"      "hb"      "pcells"  "protein"

Fyrstu línur eru:

head(d_1_3)

##   patient time status age sex bun ca   hb pcells protein
## 1       1   13      1  66   1  25 10 14.6     18       1
## 2       2   52      0  66   1  13 11 12.0    100       0
## 3       3    6      1  53   2  15 13 11.4     33       1
## 4       4   40      1  69   1  10 10 10.2     30       1
## 5       5   10      1  65   1  20 10 13.2     66       0
## 6       6    7      0  57   2  12  8  9.9     45       0

Í sýnidæmi 1.4 er borin saman lifun sjúklinga með blöðruhálskirtilskrabbamein eftir meðferð.

Comparison_of_two_treatments_for_prostatic_cancer <- read.table("Data/Comparison of two treatments for prostatic cancer.dat",header=T)
d_1_4 <- Comparison_of_two_treatments_for_prostatic_cancer
d_1_4 <- d_1_4 %>% mutate(treatmentf=factor(treatment))

Meðferðin er treatment dálkurinn og fyrstu línur eru:

head(d_1_4)

##   patient treatment time status age  shb size index treatmentf
## 1       1         1   65      0  67 13.4   34     8          1
## 2       2         2   61      0  60 14.6    4    10          2
## 3       3         2   60      0  77 15.6    3     8          2
## 4       4         1   58      0  64 16.2    6     9          1
## 5       5         2   51      0  65 14.1   21     9          2
## 6       6         1   51      0  61 13.5    8     8          1

3.2.1 A model for comparison of two groups

Byrjum á að bera saman tvo hópa og notum gögnin úr sýnidæmi 1.4. Meðferðirnar eru tvær:

table(d_1_4$treatmentf)

## 
##  1  2 
## 18 20

Við eigum alltaf að byrja á að meta fjölda atburða, eftirfylgnitíma og tíðni atburða á tímaeiningu.

r0 <- d_1_4 %>% summarise(n=n(),d=sum(status),
                                            V=sum(time),lambda=d/V,se.lambda=sqrt(d)/V)
r0

##    n d    V      lambda   se.lambda
## 1 38 6 1890 0.003174603 0.001296026

r <- d_1_4 %>% group_by(treatmentf) %>% summarise(n=n(),
                                            d=sum(status),
                                            V=sum(time),lambda=d/V,se.lambda=sqrt(d)/V)
r

## # A tibble: 2 x 6
##   treatmentf     n     d     V   lambda se.lambda
##   <fct>      <int> <int> <int>    <dbl>     <dbl>
## 1 1             18     5   821 0.00609   0.00272 
## 2 2             20     1  1069 0.000935  0.000935

Við sjáum að tíðni atburða er lægri fyrir meðferð tvö og hættuhlutfallið er

exp(diff(log(r$lambda)))

## [1] 0.1536015

Reyndar er þetta mat það sama og ef við miðum við veldisdreifingu á lifunartímanum. Einfalt er að meta hættuhlutfallið með flexurvreg fallinu í flexurv pakkanum:

f0 <- flexsurvreg(Surv(time,status) ~ 1,data=d_1_4,dist="exponential")
f0

## Call:
## flexsurvreg(formula = Surv(time, status) ~ 1, data = d_1_4, dist = "exponential")
## 
## Estimates: 
##       est      L95%     U95%     se     
## rate  0.00317  0.00143  0.00707  0.00130
## 
## N = 38,  Events: 6,  Censored: 32
## Total time at risk: 1890
## Log-likelihood = -40.51544, df = 1
## AIC = 83.03087

f1 <- flexsurvreg(Surv(time,status) ~ treatmentf,data=d_1_4,dist="exponential")
f1

## Call:
## flexsurvreg(formula = Surv(time, status) ~ treatmentf, data = d_1_4, 
##     dist = "exponential")
## 
## Estimates: 
##              data mean  est       L95%      U95%      se        exp(est)
## rate               NA    0.00609   0.00253   0.01463   0.00272        NA
## treatmentf2   0.52632   -1.87339  -4.02043   0.27364   1.09545   0.15360
##              L95%      U95%    
## rate               NA        NA
## treatmentf2   0.01795   1.31474
## 
## N = 38,  Events: 6,  Censored: 32
## Total time at risk: 1890
## Log-likelihood = -38.4799, df = 2
## AIC = 80.95981

Í fyrsta líkaninu er engin skýribreyta og fæst þá tíðnin fyrir allan hópinn. Berið saman við r0 að ofan.

Í seinna líkaninu býr flexurvreg til dummy breytu þannig að ef treatment er 1 fær dummy breytan gildið 0 en ef treatment er 2 fær dummy breytan gildið 1. Grunnhættufallið sem flexurvreg metur er fyrir öll gildi á skýribreytum sem 0. Hér er bara ein skýribreyta og þegar hún er 0 gildið að treatment er 1.

Að ofan gefur línan rate þá matið á lambda í veldisdreifingunni þegar treatment er 1. Síðan gefur línan treatmentf2 mismuninn á log-rate á treatment=2 miðað við treatment=1.

beta <- diff(log(r$lambda))
beta

## [1] -1.873394

Hættuhlutfallið er

exp(beta)

## [1] 0.1536015

Öryggisbilið er vítt og inniheldur 1. Það næst ekki að sýna fram á tölfræðilega marktækan mun hér með Wald prófinu.

exp(confint(f1))[2,]

##      2.5 %     97.5 % 
## 0.01794531 1.31474020

Log-likelihood prófið er aflmeira og rétt nær að sýna fram á martkækan mun

ll <- -2*(logLik(f0)-logLik(f1))
ll

## 'log Lik.' 4.071062 (df=1)

1-pchisq(ll,1)

## 'log Lik.' 0.04362384 (df=1)

Athugið að hættuhlutfallið er um 85% lægra í treatment=1 miðað við treatment=2! Það væri til mikils að rannsaka þetta betur með stærra þýði.

Hér getum við skrifað \(h_0(t) = \lambda\) fyrir treatment=1 og \(h_1(t) = \exp(\beta) h_0(t)\) fyrir treatment=2.

Þetta er einfaldasta proportional hazards líkanið.

Við getum valið annað form á \(h_0(t)\) (t.d. Weibull) eða haft óstikað mat á \(h_0(t)\) og erum við þá komin með líkan Cox.

Við höfum þegar kynnst alveg óstikuðu mati á lifunartíma. Við skulum rifja það upp og teikna stikaða matið með óstikaða matinu úr aðferð Kaplan-Meier.

Við höfum að \(h_0(t) = \lambda\). Þá er \(H_0(t) = \lambda t\) og \(S_0(t) = \exp(-\lambda t)\). Svo er \(h_1(t) = \exp(\beta) h_0(t)\) og þá \(H_1(t) = \exp(\beta) \lambda t\) og \(S_1(t) =\exp(-\exp(\beta) \lambda t) = \exp(-\lambda t) ^ {\exp(\beta)} = S_0(t) ^{\exp(\beta)}\).

s1 <- survfit(Surv(time,status) ~ treatmentf,data=d_1_4)
plot(s1)
t <- 0:70
lines(t,exp(-0.00609 * t),col="blue")
lines(t,exp(-0.00609 * t) ^ exp( -1.87339 ),col="red")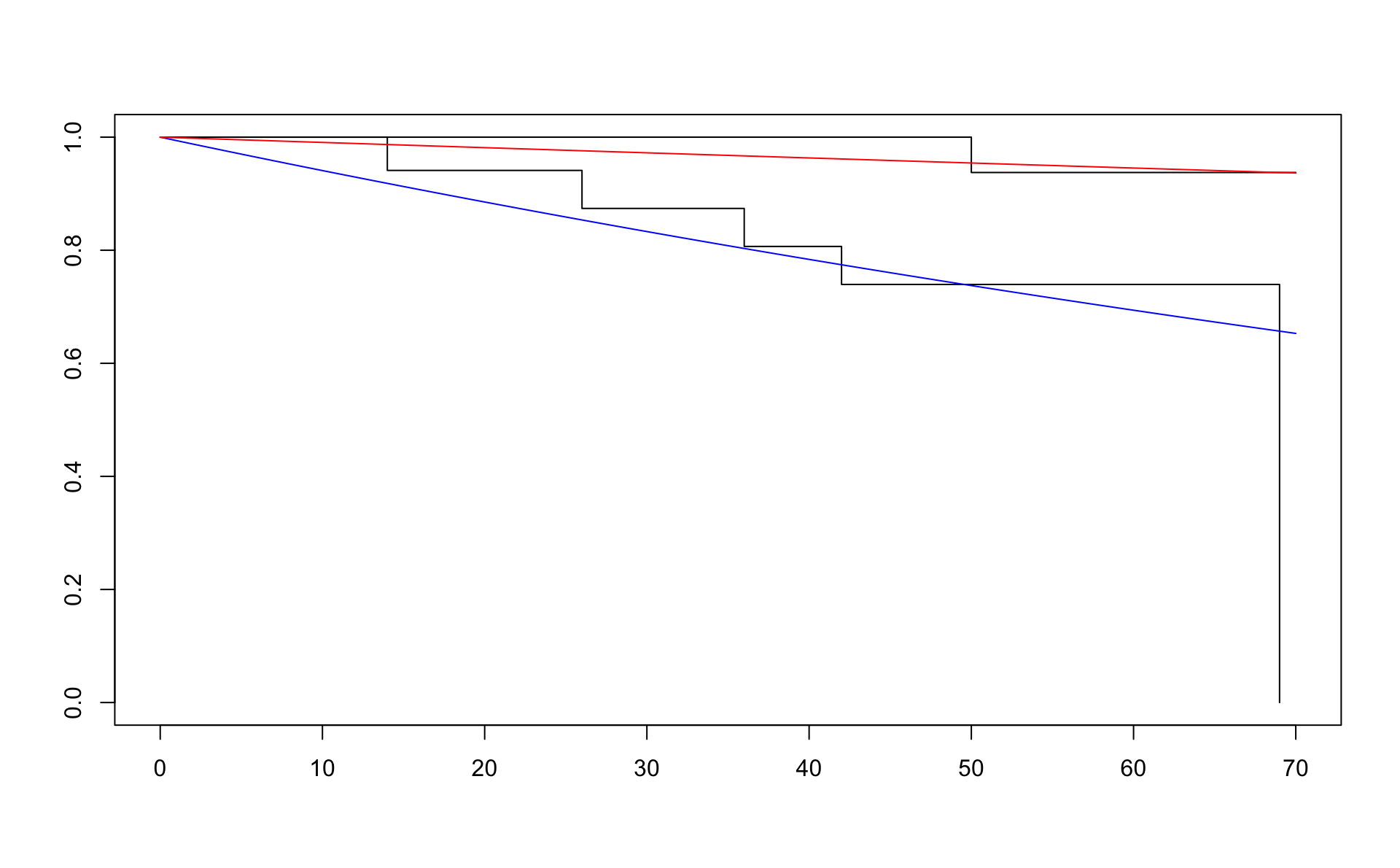

Óstikað próf á mun má milli meðferða væri gert með log rank:

survdiff(Surv(time,status) ~ treatmentf,data=d_1_4)

## Call:
## survdiff(formula = Surv(time, status) ~ treatmentf, data = d_1_4)
## 
##               N Observed Expected (O-E)^2/E (O-E)^2/V
## treatmentf=1 18        5     2.47      2.58      4.42
## treatmentf=2 20        1     3.53      1.81      4.42
## 
##  Chisq= 4.4  on 1 degrees of freedom, p= 0.04

Hér fæst marktækt lægri tíðni atburða í treatment 2 miðað við treatment 1.

Til að undirbúa okkur fyrir Cox líkanið skulum við skoða niðurstöðuna úr því líkani með coxph. Hér er \(h_0(t)\) óstikað og við fáum bara hlutfallið \(\exp(\beta)\) á milli \(h_1(t)\) og \(h_0(t)\).

coxph(Surv(time,status) ~ treatmentf,data=d_1_4,ties = "breslow")

## Call:
## coxph(formula = Surv(time, status) ~ treatmentf, data = d_1_4, 
##     ties = "breslow")
## 
##                coef exp(coef) se(coef)      z      p
## treatmentf2 -1.9780    0.1384   1.0982 -1.801 0.0717
## 
## Likelihood ratio test=4.55  on 1 df, p=0.03293
## n= 38, number of events= 6

Niðurstöðurnar eru líkar niðurstöðunni að ofan úr veldisdreifingunni, en ekki alveg eins. Við lærum seinna hvernig við náum í matið á \(h_0(t)\) úr Cox líkaninu.

3.2.2 The general proportional hazards model

Almennt skrifum við proportional hazards líkanið svona

\[ h(t) = h_0(t) \exp(\beta_1 x_1 + \cdots + \beta_p x_p). \]

Með því að deila með \(h_0(t)\) og taka logra fæst:

\[ \log \left( \frac{h(t)}{h_0(t)} \right) = \beta_1 x_1 + \cdots + \beta_p x_p. \]

Með öðrum orðum er logrinn af áhættuhlutfallinu línuleg samantekt af skýribreytunum.

Farið er með skýribreytur alveg eins í öðrum línulegum líkönum eins og aðhvarfsgreiningu og tvíkosta aðhvarfsgreiningu.

3.3 Fitting the Cox regression model

Hér er stuttlega sýnt hvernig eitt hættuhlutfall er fengið með Cox líkaninu.

Prognosis_for_women_with_breast_cancer <- read.table("Data/Prognosis for women with breast cancer.dat",
                                                    header=T)
d_1_2 <- Prognosis_for_women_with_breast_cancer
d_1_2 <- d_1_2 %>% mutate(stainf = factor(stain))

En fyrst alltaf að skoða tíðni atburða:

r <- d_1_2 %>% group_by(stainf) %>% summarise(n=n(),
                                            d=sum(status),
                                            V=sum(time),lambda=d/V,se.lambda=sqrt(d)/V)
r

## # A tibble: 2 x 6
##   stainf     n     d     V  lambda se.lambda
##   <fct>  <int> <int> <int>   <dbl>     <dbl>
## 1 1         13     5  1652 0.00303   0.00135
## 2 2         32    21  2679 0.00784   0.00171

r$lambda

## [1] 0.003026634 0.007838746

diff(log(r$lambda))

## [1] 0.9516276

exp(diff(log(r$lambda)))

## [1] 2.589922

Svo Cox líkanið:

f2 <- coxph(Surv(time, status) ~ stainf,data=d_1_2,ties = "breslow")
f2

## Call:
## coxph(formula = Surv(time, status) ~ stainf, data = d_1_2, ties = "breslow")
## 
##           coef exp(coef) se(coef)     z      p
## stainf2 0.9080    2.4794   0.5009 1.813 0.0699
## 
## Likelihood ratio test=3.87  on 1 df, p=0.04911
## n= 45, number of events= 26

exp(coef(f2))

##  stainf2 
## 2.479398

exp(confint(f2))

##             2.5 %   97.5 %
## stainf2 0.9288808 6.618086

Næst skoðum við fjölbreytulíkan úr multiple myaloma gögnunum.

skim(d_1_3)

Table 3.1: Data summary

Name	d_1_3
Number of rows	48
Number of columns	10
_______________________
Column type frequency:
numeric	10
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
patient	1	24.50	14.00	1.0	12.75	24.5	36.25	48.0	▇▇▇▇▇
time	1	23.38	23.72	1.0	6.75	14.5	37.00	91.0	▇▁▂▁▁
status	1	0.75	0.44	0.0	0.75	1.0	1.00	1.0	▂▁▁▁▇
age	1	62.90	6.96	50.0	58.75	62.5	68.25	77.0	▅▇▇▇▃
sex	1	1.40	0.49	1.0	1.00	1.0	2.00	2.0	▇▁▁▁▅
bun	1	33.92	35.91	6.0	13.75	21.0	39.25	172.0	▇▂▁▁▁
ca	1	9.94	1.45	8.0	9.00	10.0	10.00	15.0	▇▆▃▁▁
hb	1	10.25	2.79	4.9	8.65	10.2	12.57	14.6	▃▂▇▅▆
pcells	1	42.94	30.02	3.0	21.25	33.0	63.00	100.0	▇▇▆▃▅
protein	1	0.31	0.47	0.0	0.00	0.0	1.00	1.0	▇▁▁▁▃

Hér setjum við allar breytur inn. En hugsanlea mundum við laga þær til. Breyta í factor og miðja en það kemur síðar:

f4 <- coxph(Surv(time,status) ~ age + sex + bun + ca + hb  + pcells + protein,data = d_1_3,ties="breslow" )
f4

## Call:
## coxph(formula = Surv(time, status) ~ age + sex + bun + ca + hb + 
##     pcells + protein, data = d_1_3, ties = "breslow")
## 
##              coef exp(coef)  se(coef)      z        p
## age     -0.019358  0.980828  0.027924 -0.693 0.488159
## sex     -0.250899  0.778101  0.402286 -0.624 0.532836
## bun      0.020826  1.021044  0.005929  3.513 0.000443
## ca       0.013125  1.013211  0.132442  0.099 0.921061
## hb      -0.135241  0.873506  0.068891 -1.963 0.049635
## pcells  -0.001594  0.998407  0.006577 -0.242 0.808533
## protein -0.640438  0.527061  0.426687 -1.501 0.133367
## 
## Likelihood ratio test=16.24  on 7 df, p=0.02302
## n= 48, number of events= 36

Frank Harrell er líka með fall fyrir Cox likanið. Það gefur meiri upplýsingar t.d. R2 og Dxy sem er skylt concordance index C þannig að \(C = 0.5(Dxy+1)\)

f5 <- cph(Surv(time,status) ~ age + sex + bun + ca + hb  + pcells + protein,data = d_1_3,ties="breslow" )
f5

## Cox Proportional Hazards Model
##  
##  cph(formula = Surv(time, status) ~ age + sex + bun + ca + hb + 
##      pcells + protein, data = d_1_3, ties = "breslow")
##  
##                      Model Tests       Discrimination    
##                                           Indexes        
##  Obs        48    LR chi2     17.53    R2       0.309    
##  Events     36    d.f.            7    Dxy      0.410    
##  Center -2.219    Pr(> chi2) 0.0143    g        0.940    
##                   Score chi2  25.59    gr       2.561    
##                   Pr(> chi2) 0.0006                      
##  
##          Coef    S.E.   Wald Z Pr(>|Z|)
##  age     -0.0181 0.0278 -0.65  0.5165  
##  sex     -0.2495 0.4031 -0.62  0.5360  
##  bun      0.0227 0.0061  3.71  0.0002  
##  ca       0.0133 0.1327  0.10  0.9204  
##  hb      -0.1330 0.0685 -1.94  0.0523  
##  pcells  -0.0014 0.0066 -0.21  0.8366  
##  protein -0.6833 0.4294 -1.59  0.1116  
##

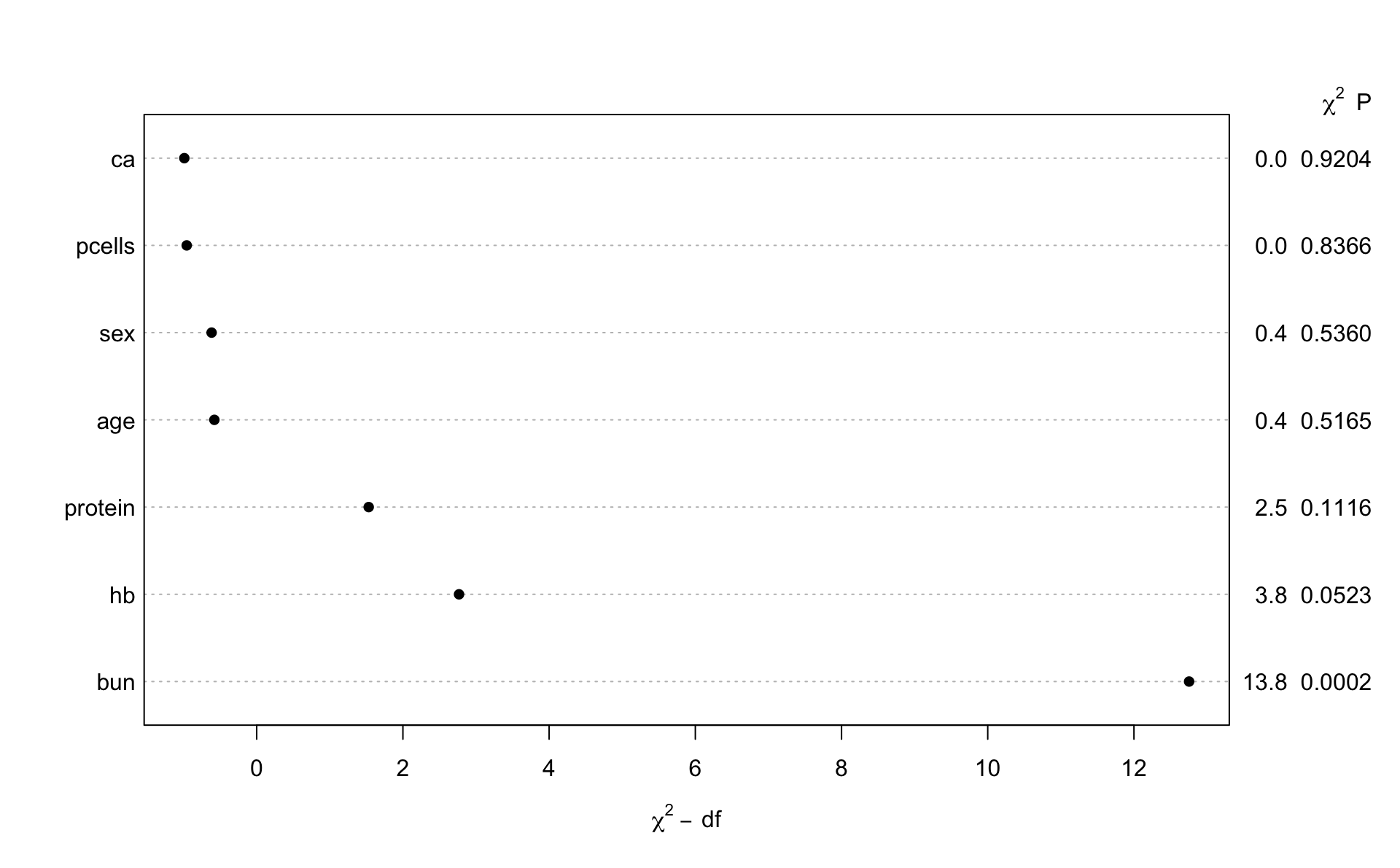
Svo er mjög gagnlegt að bera saman spágetu breytanna út frá kí-kvaðrat gildum og bera saman.

Hér sést í fljótu bragði að bun, hb og e.t.v. protein skipta mestu máli.

plot(anova(f5))