Applying a Gaussian AR(1) Copula to Generalized Extreme Value Margins

A simulation study of the differences between AR(1) copula and i.i.d copula

Another step in my PhD studies is to apply multivariate copulas to data with Generalized Extreme Value marginal distributions. This is important to enable us to model dependence on the data leve, as opposed to the latent (parameter) level.

english
R
phd
stan
bayesian
spatial statistics
copulas
Author
Affiliation

Brynjólfur Gauti Guðrúnar Jónsson

Tölfræði, Raunvísindadeild Háskóla Íslands

Published

February 6, 2024

Code 
library(gt)
library(tidyverse)
library(patchwork)
library(bggjphd)
theme_set(theme_bggj())

Introduction

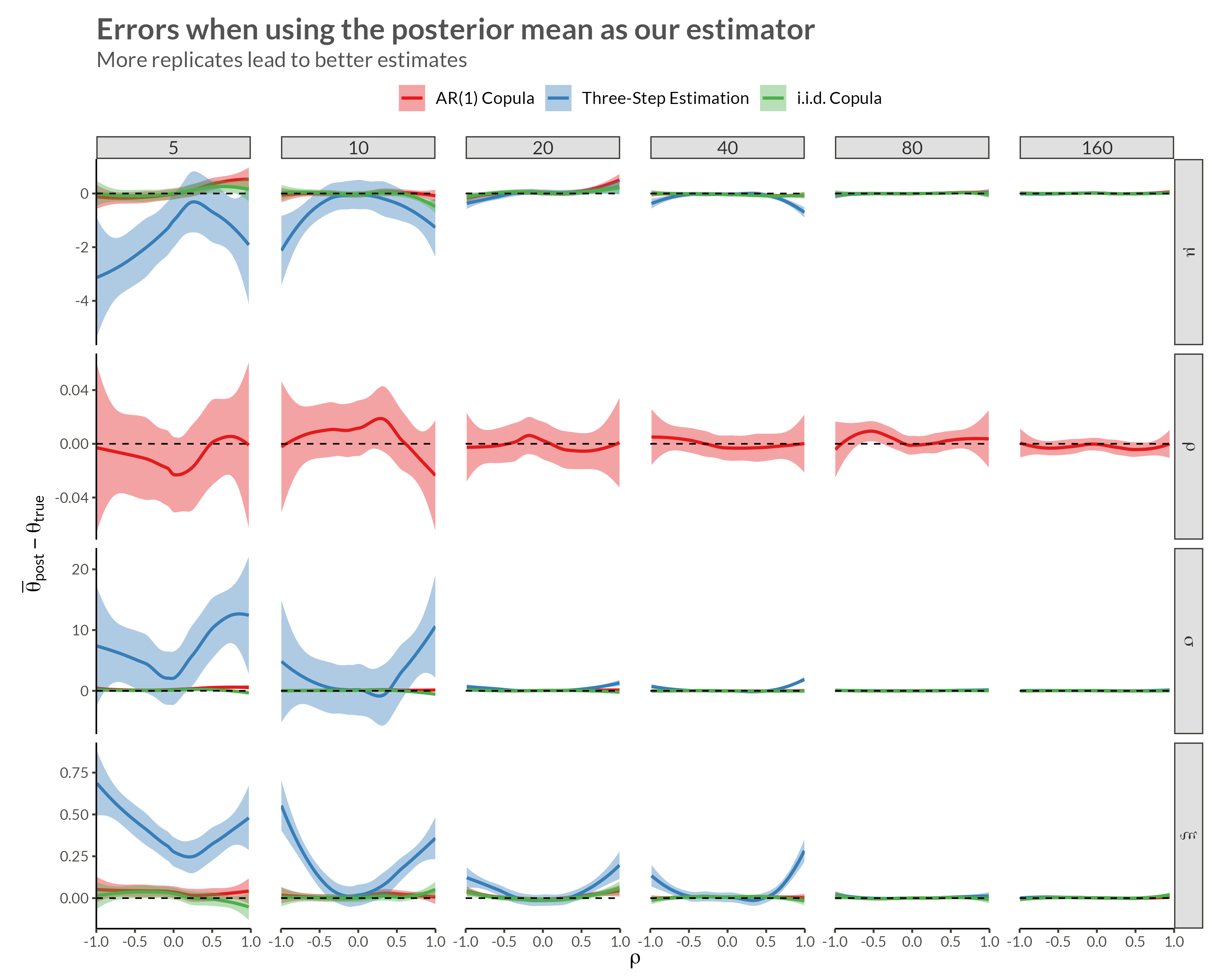
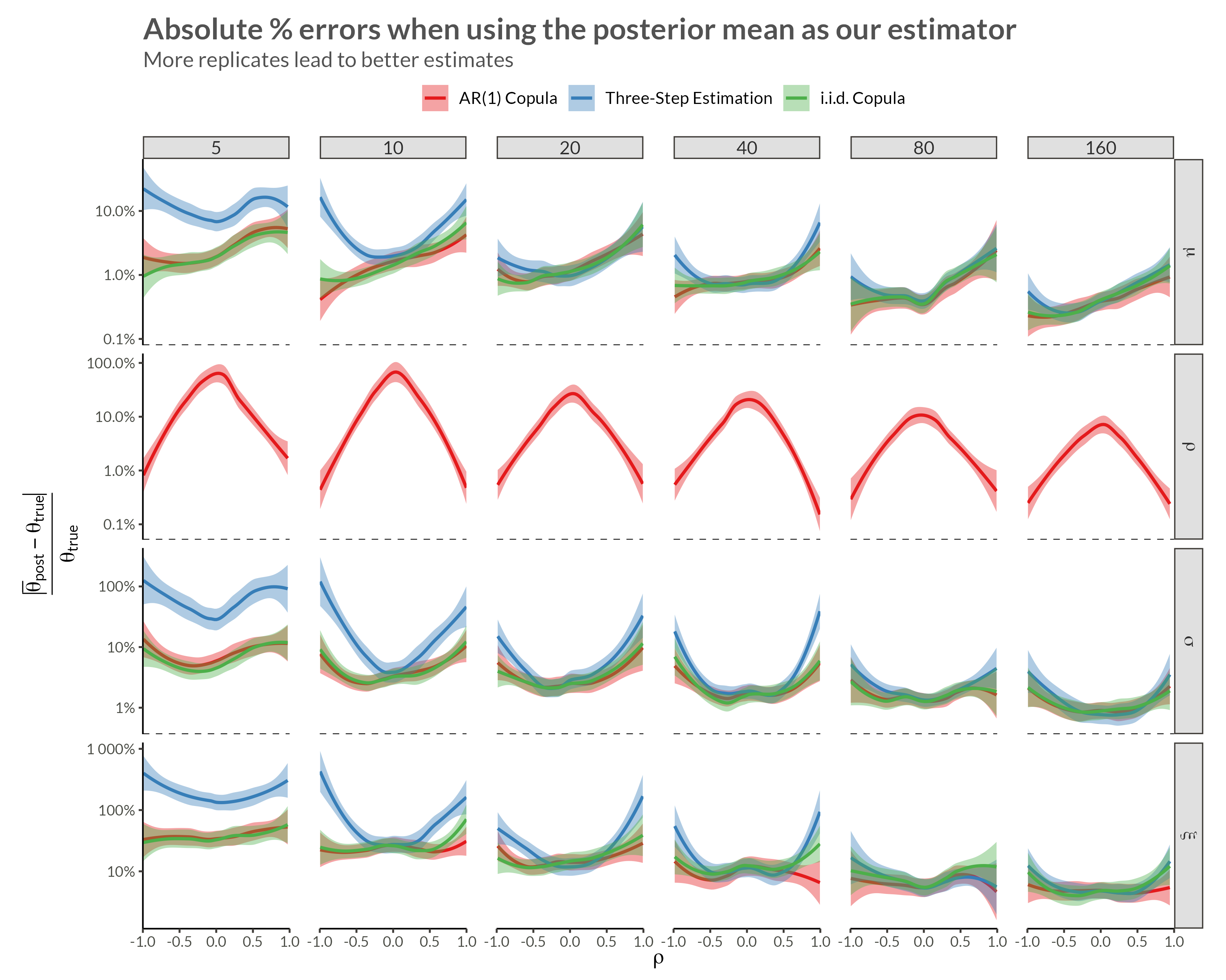
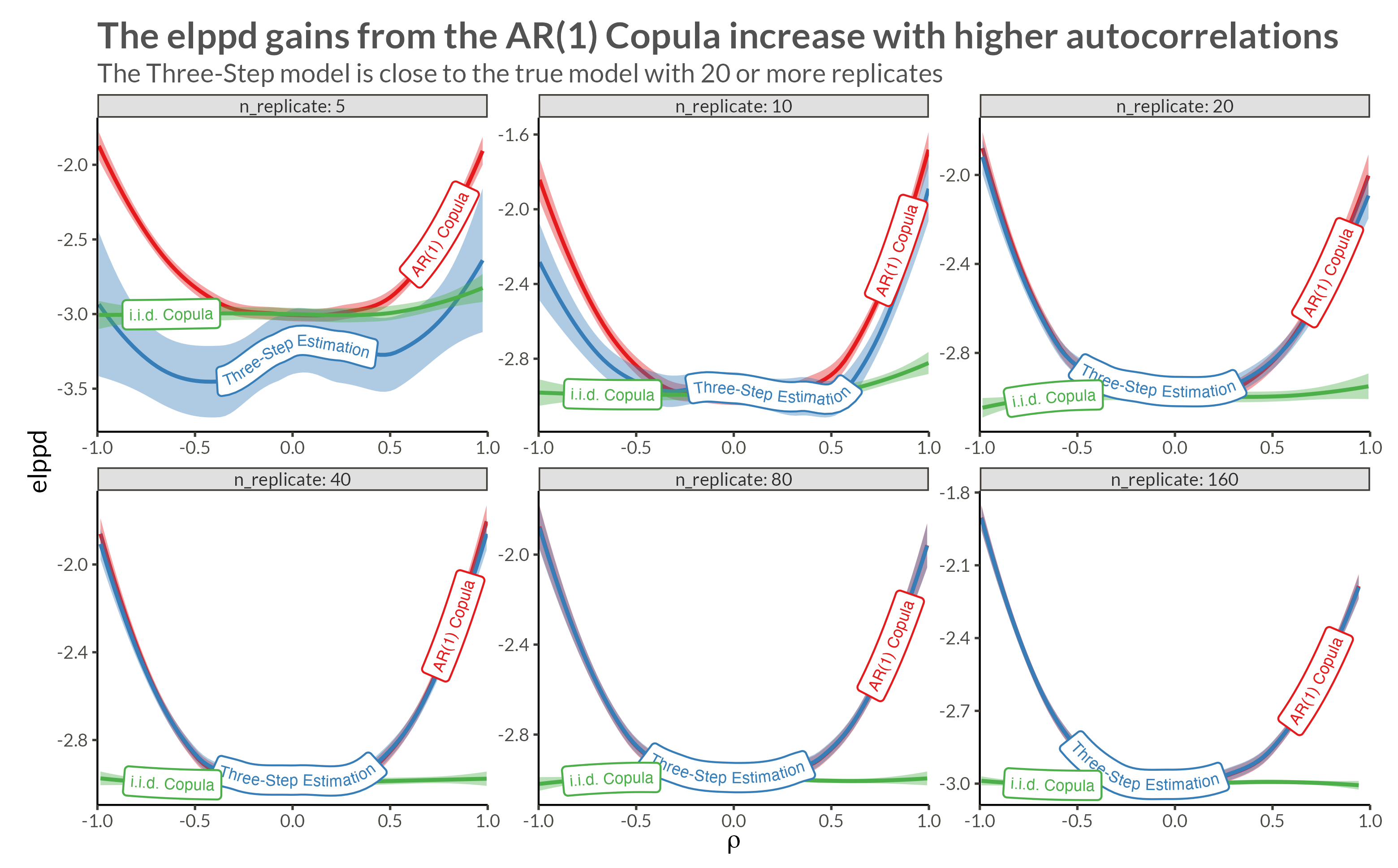
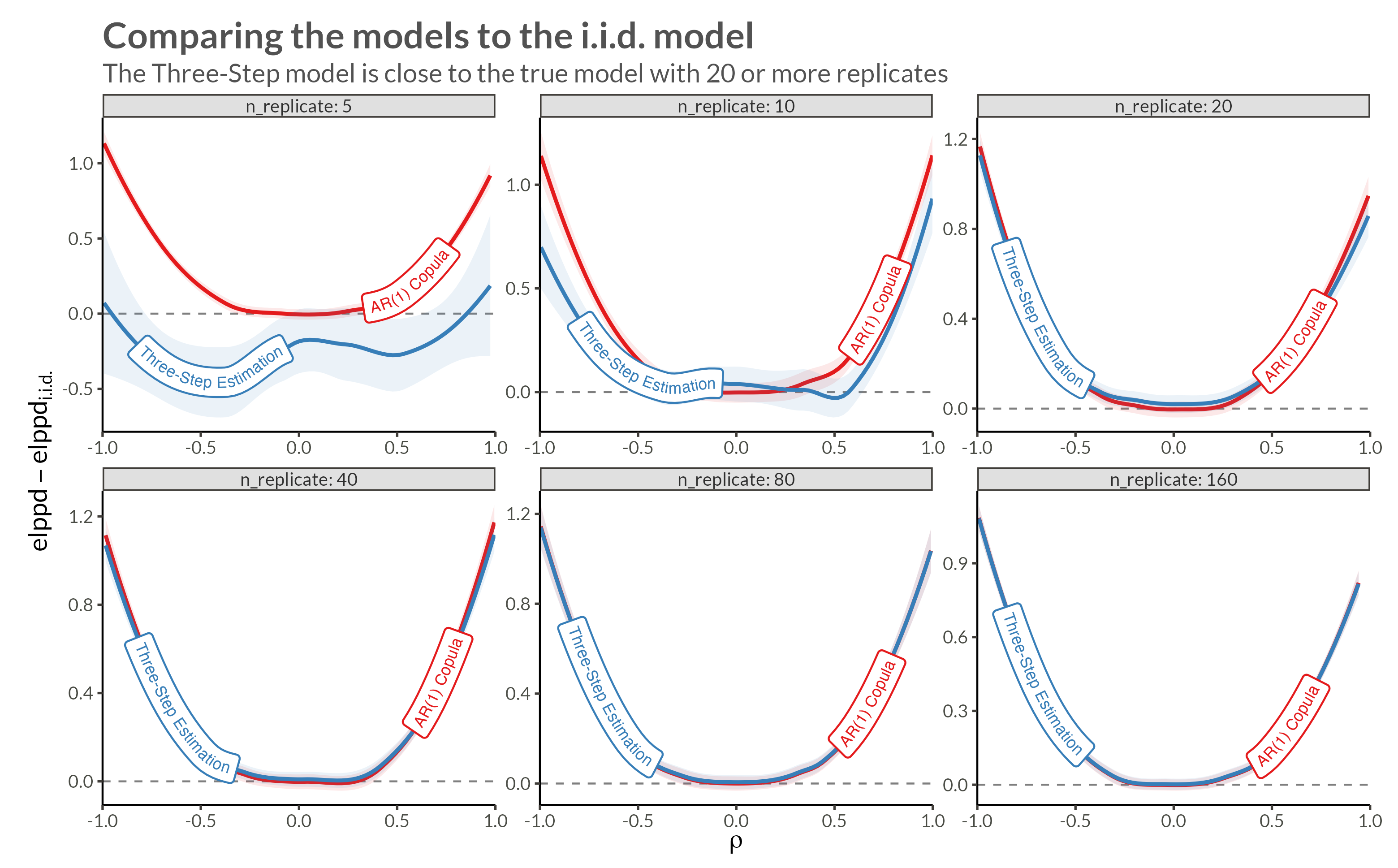
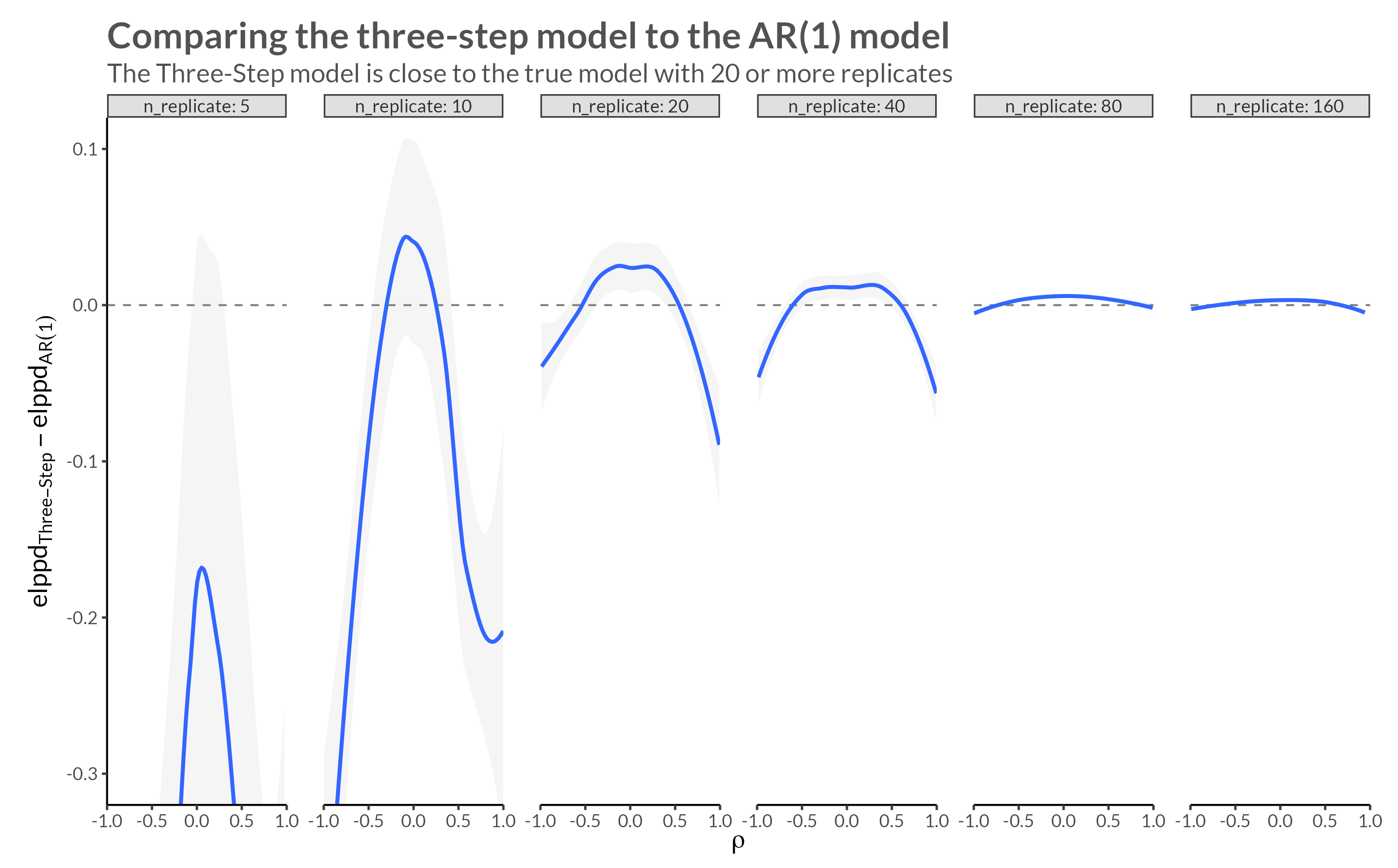
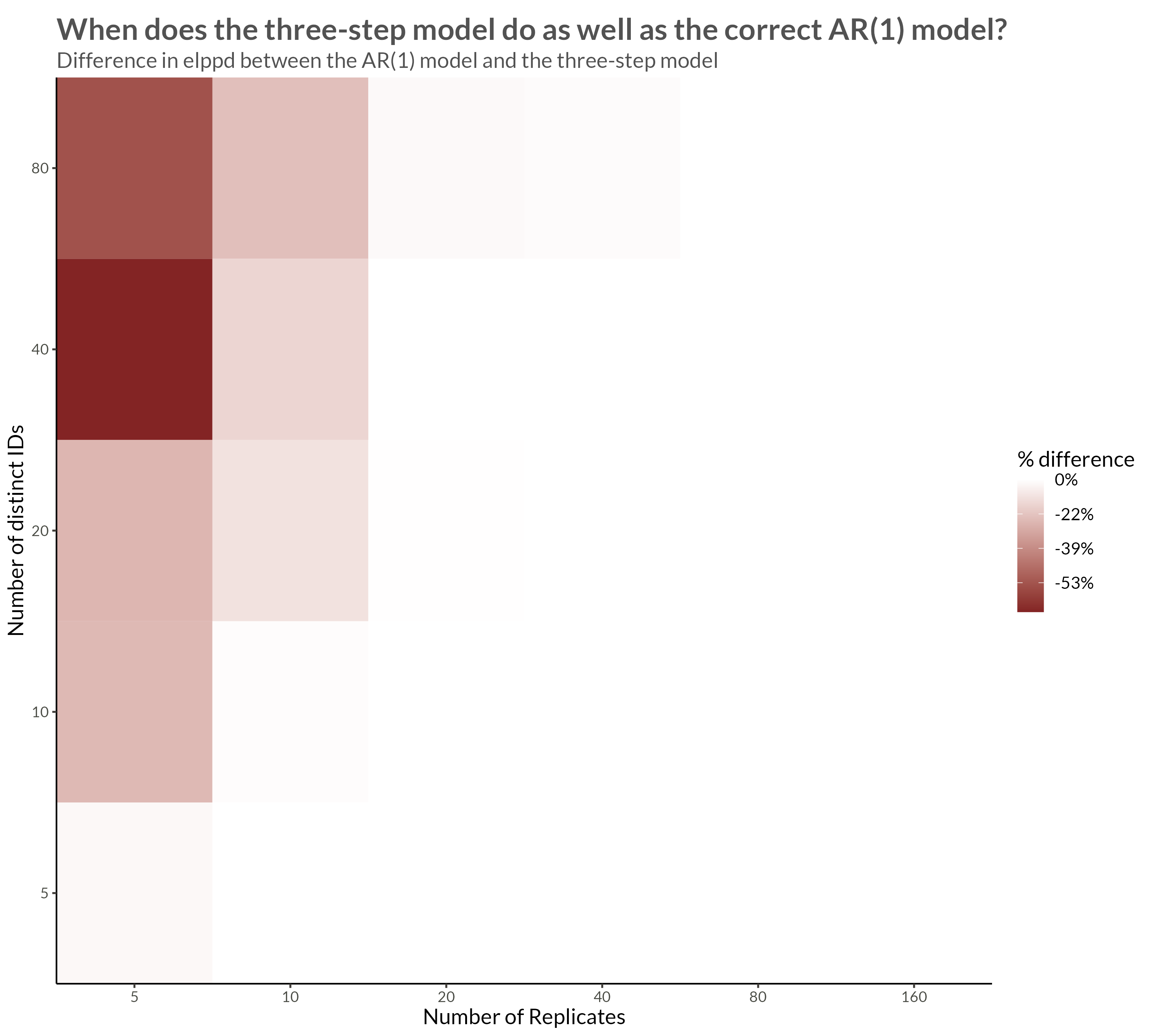
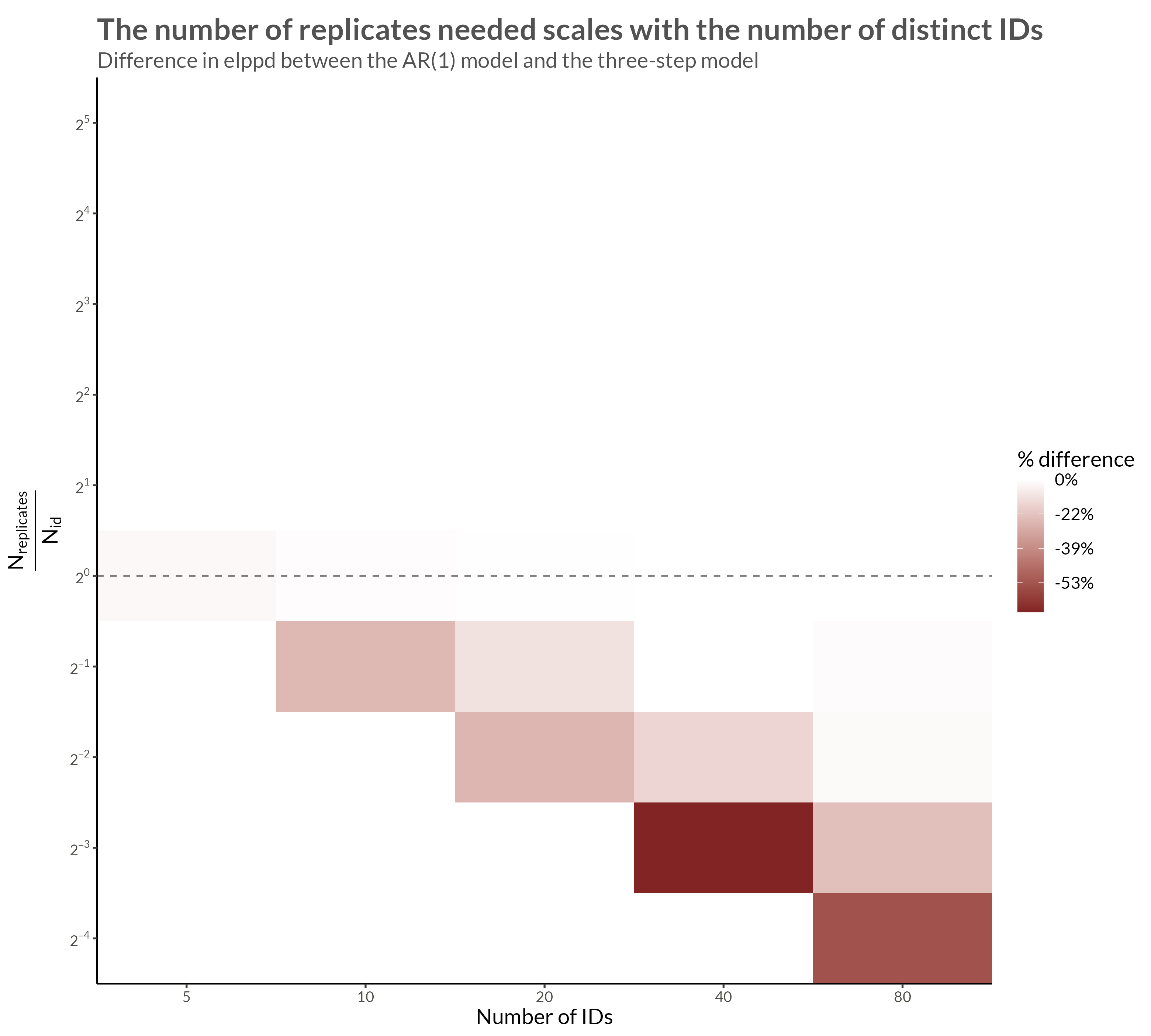
In a previous post, I wrote about applying the BYM2 model to spatially dependent Generalized Extreme Value (GEV) data and mentioned in passing that I was working on applying copulas as well. In this post I will outline and show results from a simulation study I’ve been running where I:

  • Learn how to generate multivariate data that have GEV margins and dependence structures based on an AR(1) Gaussian copula
  • Learn how to code simple Gaussian copulas in Stan
  • Compare the model fits of the AR(1) copula to a model where I assume i.i.d. observations

Copulas

In the book Elements of Copula Modeling with R, Hofert et al. (2018) define a copula as

Hofert, Marius, Ivan Kojadinovic, Martin Mächler, and Jun Yan. 2018. Elements of Copula Modeling with R. Use R! Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-89635-9.

a multivariate distribution function with standard uniform univariate margins, that is, U(0, 1) margins.

So, a Copula is any multivariate distribution whose margins is U(0,1 ) distributed. A simple example is the independence copula

\[ \Pi(u) = \prod_{j=1}^{d}{u_j}, \quad \mathbf U \in [0, 1]^d. \]

The central theorem of copula theory is Sklar’s theorem (Sklar 1996) [the original paper is from 1959]. The theorem basically states that for any d-dimensional distribution function, \(H\), with univariate margins \(F_1, \dots, F_d\), there exists a d-dimensional copula \(C\) such that

Sklar, A. 1996. “Random Variables, Distribution Functions, and Copulas: A Personal Look Backward and Forward.” Lecture Notes-Monograph Series 28: 1–14. https://www.jstor.org/stable/4355880.

\[ H(\mathbf x) = C(F_1(x_1), \dots, F_d(x_d)). \]

Alternatively, we can write

\[ C(\mathbf u) = H(F_1^{-1}(u_1), \dots, F_d^{-1}(u_d)) \]

Gaussian Copula

The Gaussian family of copulas can be written

\[ C(\mathbf u | R) = \Phi_d\left(\Phi^{-1}(u_1), \dots, \Phi^{-1}(u_d) \vert R \right), \quad \mathbf u \in [0, 1]^d, \]

where R is a \(d\times d\) correlation matrix, \(\Phi_d\) is the CDF of a d-dimensional multivariate Gaussian with mean \(\mathbf 0\) and covariance matrix \(R\), and \(\Phi\) is the CDF of a standard Gaussian.

Its density is

\[ c(\mathbf u \vert R) = \frac{\phi_d\left(\Phi^{-1}(u_1), \dots, \Phi^{-1}(u_d) \vert R \right)}{ \prod_{j=1}^{d}{\phi\left( \Phi^{-1}(u_j) \right)}}, \quad \mathbf u \in [0, 1]^d, \]

where \(\phi_d\) is the density of the same multivariate Gaussian, and \(\phi\) is the density of a standard gaussian.

Sampling from the Gaussian copula

Given the \(d\times d\) correlation matrix, \(R\):

  1. Compute the Cholesky factor \(L\) of the correlation matrix, \(R\).
  2. Sample \(Z_1, \dots, Z_d \overset{iid}{\sim}\mathrm{Normal}(0, 1)\).
  3. Compute \(X = LZ\).
  4. Return \(\mathbf u = \left(\Phi(X_1), \dots, \Phi(X_d)\right)\)

We can then make the margins \(u_1, \dots, u_d\) follow any distribution (f.ex. the GEV distribution) by applying its quantile function.

Example

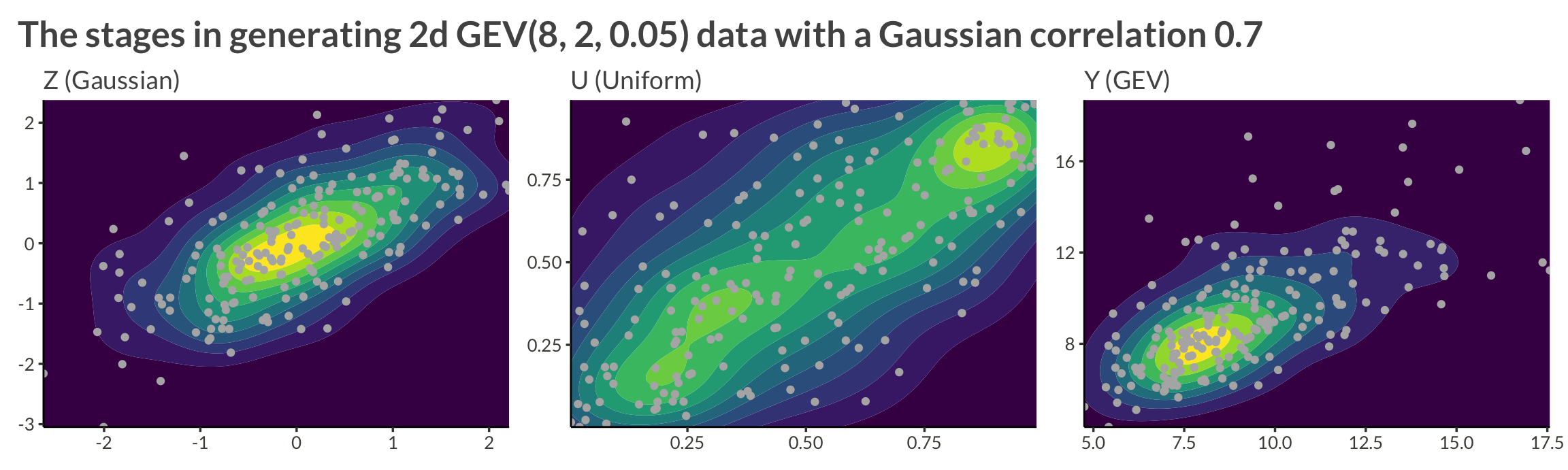
Let’s sample from a two-dimensional process with GEV(8, 2, 0.05) margins and a Gaussian copula with correlation \(\rho = 0.7\).

Code 
R <- matrix(c(1, 0.7, 0.7, 1), nrow = 2)
set.seed(1)
X <- mvtnorm::rmvnorm(
  n = 200,
  sigma = R
)

X |> 
  as_tibble() |> 
  mutate(
    id = row_number()
  ) |> 
  pivot_longer(c(-id), names_to = "variable", values_to = "Z") |> 
  mutate(
    U = pnorm(Z),
    Y = evd::qgev(U, loc = 8, scale = 2, shape = 0.05)
  ) |> 
  pivot_longer(c(-id, -variable)) |> 
  pivot_wider(names_from = variable, values_from = value) |>
  mutate(
    name = fct_relevel(name, "Z", "U", "Y") |> 
      fct_recode(
        "Z (Gaussian)" = "Z",
        "U (Uniform)" = "U",
        "Y (GEV)" = "Y"
      )
  ) |> 
  group_by(name2 = name) |> 
  group_map(
    function(data, ...) {
      data |> 
        ggplot(aes(V1, V2)) +
        geom_density_2d_filled() +
        geom_point(col = "grey70") +
        coord_cartesian(expand = FALSE) +
        theme(legend.position = "none") +
        labs(
          x = NULL,
          y = NULL,
          subtitle = data$name
        )
    }
  ) |> 
  wrap_plots() +
  plot_annotation(
    title = "The stages in generating 2d GEV(8, 2, 0.05) data with a Gaussian correlation 0.7"
  )

Methods

Data

R scripts used for simulating the data

The simulated data have GEV margins and an AR(1) Gaussian copula. The steps in simulating the data are as follows.

  1. Generate a correlation matrix, R, based on an AR(1) process
  2. Generate multivariate normal variates with mean zero and covariance matrix R.
  3. Transform to GEV by applying normal CDF and GEV quantile functions

1. Correlation Matrix

First, a correlation matrix is generated that encodes an AR(1) process with correlation \(\rho\). To create this correlation matrix, we specify the precision matrix, \(Q\), via

\[ Q = \frac{1}{1 - \rho^2}\begin{bmatrix} 1 & -\rho & \dots & \dots & \vdots\\ -\rho & 1 + \rho^2 & -\rho & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots &-\rho & 1 + \rho^2 & -\rho \\ \vdots & \dots & \dots & -\rho & 1 \end{bmatrix}. \]

This gives us the correlation matrix, R, where

\[ R = Q^{-1} = \begin{bmatrix} 1 & \rho & \rho^2 & \dots & \rho^n\\ \rho & 1 & \rho & \ddots & \rho^{n-1} \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ \rho^{n-1} & \ddots &\rho & 1 & \rho \\ \rho^n & \dots & \dots & \rho & 1 \end{bmatrix}. \]

Code 
make_AR_cor_matrix_1d <- function(n_id, rho = 0.5) {
  P <- matrix(
    0, 
    nrow = n_id,
    ncol = n_id
  )
  diag(P) <- 1
  for (i in seq(1, n_id - 1)) {
    P[i, i + 1] <- -rho
  }
  
  for (i in seq(2, n_id)) {
    P[i, i - 1] <- -rho
  }
  
  for (i in seq(2, n_id - 1)) {
    P[i, i] <- 1 + rho^2
  }
  
  P <- P / (1 - rho^2)
  
  P_cor <- solve(P)
  P_cor
}

n_id <- 5
rho <- 0.5

R <- make_AR_cor_matrix_1d(n_id = n_id, rho = rho)
R
       [,1]  [,2] [,3]  [,4]   [,5]
[1,] 1.0000 0.500 0.25 0.125 0.0625
[2,] 0.5000 1.000 0.50 0.250 0.1250
[3,] 0.2500 0.500 1.00 0.500 0.2500
[4,] 0.1250 0.250 0.50 1.000 0.5000
[5,] 0.0625 0.125 0.25 0.500 1.0000

2. Generating Multivariate Normal Data

We then use the well-known fact that if

\[ \mathbf X \sim \mathrm{MVNorm}\left(\boldsymbol \mu, \Sigma\right), \]

then

\[ \boldsymbol X = \boldsymbol \mu + L \boldsymbol Z, \]

where \(\boldsymbol Z \sim \mathrm{Normal}(\boldsymbol 0, I)\) and \(L\) is the Cholesky decomposition of \(R\), or \(LL^T = \Sigma\).

In our case, we want \(\mathbf X\) to have mean 0 and covariance matrix \(R\), so we write

\[ \mathbf X = L\mathbf Z \]

where \(LL^T = R\).

We can skip the manual Cholesky factorization and simply use the {mvtnorm} package.

Code 
sample_gaussian_variables <- function(cor_matrix, n_replicates) {
  mvtnorm::rmvnorm(
    n = n_replicates,
    sigma = cor_matrix
  )
}

R |> 
  sample_gaussian_variables(n_replicates = 1)
         [,1]     [,2]       [,3]       [,4]       [,5]
[1,] 1.427875 1.837133 -0.1348893 -0.3970323 -0.4613493

We will want more than one observation from each “site”, so we write a helped function for tidying this output into a tibble.

Code 
tidy_mvgauss <- function(mvnorm_matrix) {
  colnames(mvnorm_matrix) <- seq_len(ncol(mvnorm_matrix))
  
  mvnorm_matrix |> 
    dplyr::as_tibble() |> 
    dplyr::mutate(
      replicate = dplyr::row_number(),
      .before = `1`
    ) |> 
    tidyr::pivot_longer(
      c(-replicate),
      names_to = "id", names_transform = as.numeric,
      values_to = "Z"
    )
  
}

n_replicates <- 10
mvnorm_data <- R |> 
  sample_gaussian_variables(n_replicates = n_replicates) |> 
  tidy_mvgauss()

mvnorm_data |> 
  filter(replicate <= 5) |> 
  pivot_wider(names_from = replicate, values_from = Z) |> 
  gt() |> 
  tab_spanner(
    columns = -id,
    label = "Replicate"
  )
id Replicate
1 2 3 4 5
1 -0.4364007 -0.1443106 0.7080631 1.1388723 1.0330390
2 -0.4017539 0.6923541 0.9544816 -0.4595604 -1.3986486
3 -0.1161437 0.9328314 -0.1228664 -0.4689164 -1.1884398
4 1.0500406 -0.5297770 -0.8530328 -1.5227378 -1.0434809
5 -0.3607882 -0.5568922 1.3144552 0.1006016 -0.9255078

3. Transforming to Multivariate GEV

Now our data, \(\mathbf X\), is multivariate normal with dependence structure according to an AR(1) process, but marginally each \(X_1\) is standard normal. To transform this data to a GEV dataset, we simply use the standard normal CDF on each \(X_i\) to transform it to \([0, 1]\), then we use the GEV quantile function to transform that to a GEV distributed variable.

Code 
mvnorm_to_gev <- function(mvnorm_data, gev_params) {
  
  mvnorm_data |> 
    dplyr::mutate(
      U = pnorm(Z)
    ) |> 
    dplyr::inner_join(
      gev_params,
      by = dplyr::join_by(id)
    ) |> 
    dplyr::mutate(
      y = purrr:::pmap_dbl(
        list(U, mu, sigma, xi), 
        \(U, mu, sigma, xi) evd::qgev(p = U, loc = mu, scale = sigma, shape = xi)
      )
    )
}

gev_params <- expand_grid(
  mu = 6,
  sigma = 3,
  xi = 0.1,
  id = seq_len(n_id)
)

gev_data <- mvnorm_data |> 
  mvnorm_to_gev(gev_params = gev_params)

gev_data |> 
  select(-mu, -sigma, -xi) |> 
  gt() |> 
  opt_interactive()

Checking the data

Let’s create a function that plots heat maps for each of the three representations of the data

  • Z: The multivariate normal
  • U: The multivariate uniform
  • y: The multivariate GEV

We want the color scales to be free, so we use group_map() and wrap_plots() instead of facet_wrap()

Code 
plot_data <- function(data) {
  data |> 
    select(replicate, id, Z, U, y) |> 
    pivot_longer(c(-replicate, -id)) |> 
    mutate(
      name = fct_relevel(name, "Z", "U", "y"),
      name2 = name
    ) |> 
    group_by(name) |> 
    group_map(
      function(data, ...) {
        data |> 
          ggplot(aes(id, replicate, fill = value)) +
          geom_raster() +
          scale_fill_viridis_c() +
          coord_cartesian(expand = FALSE) +
          theme(legend.position = "none") +
          labs(
            subtitle = data$name2
          )
      }
    ) |> 
    wrap_plots() +
    plot_layout(nrow = 1) +
    plot_annotation(
      title = "Heatmaps of the three data representations",
      subtitle = "Z: Normal | U: Uniform | y: GEV"
    )
}
Code 
gev_data |> 
  plot_data()

It’s nice to wrap this process in a single function

Code 
make_data <- function(gev_params, n_replicate, rho) {
  
  make_AR_cor_matrix_1d(n_id = nrow(gev_params), rho = rho) |> 
    sample_gaussian_variables(n_replicates = n_replicate) |> 
    tidy_mvgauss() |> 
    dplyr::mutate(
      U = pnorm(Z)
    ) |> 
    dplyr::inner_join(
      gev_params,
      by = dplyr::join_by(id)
    ) |> 
    dplyr::mutate(
      y = purrr::pmap_dbl(
        list(U, mu, sigma, xi), 
        \(U, mu, sigma, xi) evd::qgev(p = U, loc = mu, scale = sigma, shape = xi)
      )
    )
}

Let’s see how the data look if we make it larger and increase the correlation

Code 
n_id <- 40
n_replicates <- 100

gev_params <- expand_grid(
  mu = 6,
  sigma = 3,
  xi = 0.1,
  id = seq_len(n_id)
)

d <- make_data(gev_params, n_replicates, rho = 0.95)

We see that with higher neighbor correlations we get obvious horizontal stripes corresponding to a large amount of dependence within each replicate.

Code 
d |> plot_data()

Modeling

R scripts used for modeling

AR(1) Model

We can fit the AR(1) model directly using Stan.

Code 
functions {
  real normal_ar1_lpdf(vector x, real rho) {
    int N = num_elements(x);
    real out;
    real log_det = - (N - 1) * (log(1 + rho) + log(1 - rho)) / 2;
    vector[N] q;
    real scl = sqrt(1 / (1 - rho^2));
    
    q[1:(N - 1)] = scl * (x[1:(N - 1)] - rho * x[2:N]);
    q[N] = x[N];
    
    out = log_det - dot_self(q) / 2;
    
    return out;
  }

  real normal_copula_ar1_lpdf(vector U, real rho) {
    int N = rows(U);
    vector[N] Z = inv_Phi(U);
    return normal_ar1_lpdf(Z | rho) + dot_self(Z) / 2;
  }

  real gev_cdf(real y, real mu, real sigma, real xi) {
    if (abs(xi) < 1e-10) {
      real z = (y - mu) / sigma;
      return exp(-exp(z));
    } else {
      real z = 1 + xi * (y - mu) / sigma;
      if (z > 0) {
        return exp(-pow(z, -1/xi));
      } else {
        reject("Found incompatible GEV parameter values");
      }
    }
  } 

  real gev_lpdf(real y, real mu, real sigma, real xi) {
    if (abs(xi) < 1e-10) {
      real z = (y - mu) / sigma;
      return -log(sigma) - z - exp(-z);
    } else {
      real z = 1 + xi * (y - mu) / sigma;
      if (z > 0) {
        return -log(sigma) - (1 + 1/xi) * log(z) - pow(z, -1/xi);
      } else {
        reject("Found incompatible GEV parameter values");
      }
    }
  }
}

data {
  int<lower = 0> n_replicate;
  int<lower = 0> n_id;
  array[n_replicate, n_id] real y;
  array[n_replicate, n_id] real y_test;
}

parameters {
  real<lower = 0> mu;
  real<lower = 0> sigma;
  real<lower = -0.5, upper = 1> xi;
  real<lower = -1, upper = 1> rho;
}

model {
  for (i in 1:n_replicate) {
    vector[n_id] U;
    for (j in 1:n_id) {    
      U[j] = gev_cdf(y[i, j] | mu, sigma, xi);
      target += gev_lpdf(y[i, j] | mu, sigma, xi);
    } 
    target += normal_copula_ar1_lpdf(U | rho);
  }
}
 
generated quantities {
  real log_lik = 0;
  {
    
    for (i in 1:n_replicate) {
      vector[n_id] U;
      for (j in 1:n_id) {
        U[j] = gev_cdf(y_test[i, j] | mu, sigma, xi);
        log_lik += gev_lpdf(y_test[i, j] | mu, sigma, xi);
      }
      log_lik += normal_copula_ar1_lpdf(U | rho);
    }
  }
  
}

i.i.d. Model

Code 
functions {
  real gev_lpdf(real y, real mu, real sigma, real xi) {
    if (abs(xi) < 1e-10) {
      real z = (y - mu) / sigma;
      return -log(sigma) - z - exp(-z);
    } else {
      real z = 1 + xi * (y - mu) / sigma;
      if (z > 0) {
        return -log(sigma) - (1 + 1/xi) * log(z) - pow(z, -1/xi);
      } else {
        reject("Found incompatible GEV parameter values");
      }
    }
  }
}

data {
  int<lower = 0> n_replicate;
  int<lower = 0> n_id;
  array[n_replicate, n_id] real y;
  array[n_replicate, n_id] real y_test;
}

parameters {
  real<lower = 0> mu;
  real<lower = 0> sigma;
  real<lower = -0.5, upper = 1> xi;
}

transformed parameters {
  
}

model {
  for (i in 1:n_replicate) {
    for (j in 1:n_id) {
      target += gev_lpdf(y[i, j] | mu, sigma, xi);
    }
  }
}

generated quantities {
  real log_lik = 0;
  {
    
    for (i in 1:n_replicate) {
      for (j in 1:n_id) {
        log_lik += gev_lpdf(y_test[i, j] | mu, sigma, xi);
      }
    }
  }
}

Two-Step Estimation

We can’t fit this model directly using one stan file. What we do is:

  1. Estimate the marginal distributions
  2. Use the empirical CDFs to transform the data into uniformly distributed variables
  3. Transform these uniformly distributed variables into standard normal variables
  4. Estimate the precision matrix using these variables
  5. Make sure the precision matrix is semi-positive definite and normalize it so that its inverse is a correlation matrix
  6. Re-estimate the marginal distributions with a gaussian copula assuming this precision matrix is known
Code 
functions {
  real gev_cdf(real y, real mu, real sigma, real xi) {
    if (abs(xi) < 1e-10) {
      real z = (y - mu) / sigma;
      return exp(-exp(z));
    } else {
      real z = 1 + xi * (y - mu) / sigma;
      if (z > 0) {
        return exp(-pow(z, -1/xi));
      } else {
        reject("Found incompatible GEV parameter values");
      }
    }
  }

  real gev_lpdf(real y, real mu, real sigma, real xi) {
    if (abs(xi) < 1e-10) {
      real z = (y - mu) / sigma;
      return -log(sigma) - z - exp(-z);
    } else {
      real z = 1 + xi * (y - mu) / sigma;
      if (z > 0) {
        return -log(sigma) - (1 + 1/xi) * log(z) - pow(z, -1/xi);
      } else {
        reject("Found incompatible GEV parameter values");
      }
    }
  }

  real normal_prec_chol_lpdf(vector x, array[] int n_values, array[] int index, vector values, real log_det) {
    int N = num_elements(x);
    int counter = 1;
    vector[N] q = rep_vector(0, N);

    for (i in 1:N) {
      for (j in 1:n_values[i]) {
        q[i] += values[counter] * x[index[counter]];
        counter += 1;
      }
    }

    return log_det - dot_self(q) / 2;

  }

  real normal_copula_prec_chol_lpdf(vector U, array[] int n_values, array[] int index, vector value, real log_det) {
    int N = rows(U);
    vector[N] Z = inv_Phi(U);

    return normal_prec_chol_lpdf(Z | n_values, index, value, log_det) + dot_self(Z) / 2;
  }

}

data {
  int<lower = 0> n_replicate;
  int<lower = 0> n_id;
  array[n_replicate, n_id] real y;
  array[n_replicate, n_id] real y_test;

  int<lower = 0> n_nonzero_chol_Q;
  real log_det_Q;
  array[n_id] int n_values;
  array[n_nonzero_chol_Q] int index;
  vector[n_nonzero_chol_Q] value;
}

parameters {
  real<lower = 0> mu;
  real<lower = 0> sigma;
  real<lower = -0.5, upper = 1> xi;
}

model {
  for (i in 1:n_replicate) {
    for (j in 1:n_id) {
      target += gev_lpdf(y[i, j] | mu, sigma, xi);
    }
  }
}
 
generated quantities {
  real log_lik = 0;
  {
    
    for (i in 1:n_replicate) {
      vector[n_id] U;
      for (j in 1:n_id) {
        U[j] = gev_cdf(y_test[i, j] | mu, sigma, xi);
        log_lik += gev_lpdf(y_test[i, j] | mu, sigma, xi);
      }
      log_lik += normal_copula_prec_chol_lpdf(U | n_values, index, value, log_det_Q);
    }
  }
  
}

Results

Estimates of GEV Parameters

Expected log predicted probability density

Comparing to the simple i.i.d. model

Differences between AR(1) and Two-Step Model